按：本系列文章的作者是本博客管理员（不是张五常教授）！

第十讲 消费者理论（上）

从今天起我们进入教材第二部分《偏好、消费与需求》的学习。这一部分的内容实际上是属于经济学中的“消费者理论”。

然而，在讲授这一部分内容之前，我要先声明：有需求定律作为公理，消费者理论实际上是——用一句很粗俗、但很生动形象的粤语俗话来形容——是“脱裤放屁、多此一举”的废物！因为消费者理论是试图把需求定律作为理论推导出来，为此它又弄出两个公理（62页上的比较公理和传递性公理），再加上一个叫“效用”的概念，弄出一套等优曲线的分析，最后通过价格变动画出价格扩展路径，推出一条需求曲线。然而，后面学下去大家就知道，由于存在着吉芬物品的困扰，这条需求曲线并不能确保一定可以向右下方倾斜，于是又得再补加一个否决吉芬物品存在的假设……总之，如果消费者理论的解释能力要跟作为公理的需求定律一样强，它必须弄一大堆新东西出来，复杂无比。根据科学方法论中的“奥克姆剃刀”原理——不同的理论如果有同样的解释力，内容越简单的越优胜——，因此需求定律胜于消费者理论！事实上，消费者理论所深深依赖的效用概念、等优曲线都是意图之物，使用时必须先设法将之转化为以事实来代替，这就大大地增加了理论应用的复杂性，造成重重的陷阱，一不小心就会掉进套套逻辑的错误之中。（诺贝尔奖得主Becker所赖以获奖的效用分析，就全是这种外观漂亮、貌似有理的套套逻辑，使几乎所有人——可能包括他自己，肯定也包括颁诺奖的人——都中了计！）而且，在实际的应用中，需求定律的解释力其实比消费者理论更强。因为正如我在第八讲《需求定律》的最后部分所指出的那样，如果对需求定律中的“价格”变量作广泛的阐释，理解为“成本”的话就也可以解释生产者的行为，而更进一步理解为“局限条件”的话，需求定律实际上可以解释一切经济学所要解释的现象！

事实上，对于实际工作者而言，消费者理论可以完全不学，也对后面的学习毫无影响。但为什么我还是要开这一讲呢？这是因为这理论的内在逻辑性很强，学习它有益于锻炼一下逻辑思维能力。也就是说，这一讲的内容大家别把它用来解释现实——基本上它是解释不了的！那看起来好像很有道理的所谓解释，其实几乎都是套套逻辑——，大家就拿它来做一场逻辑训练的游戏好了。这类似于我在第七讲里提到过的“鸡鸭同笼”的题目，现实中人们是用方程这种容易得多的方法来解这类题目的，但小学算术中让学生用算术方法来解答这类题目只是为了训练小孩的思维能力，而不是教他们真的用这种复杂、笨拙的方式解决现实中的类似问题。同样的道理，解释真实世界的现象时，大家使用需求定律这公理是最简单实用的，可别那么蠢，自讨苦吃用这一讲里的消费者理论！——至于经济学家在撰写希望能获得发表的学术论文时，为了方便使用数学公式（而不是为了真的能解释现象），那自然是使用消费者理论会更能达到他们的目的。手法高超隐蔽者，还可以像Becker那样讹个诺奖回来嘛！

打完了这一剂预防针之后，大家就来开始看一下消费者理论这葫芦里卖的是什么药。翻到书上62页。消费者理论基于两个公理，都是对人的偏好（preference，与“口味”是同一回事）作出的基本假设。一个是比较公理，说的是人能够根据他的偏好比较任意两个商品组合A和B，只有三种结果：其一是人认为A优于B，其二是人认为B优于A，其三是人认为A与B等优。另一个是传递性公理，是指人对商品组合的偏好是可以传递的，即如果他认为A优于B，又认为B优于C，则他一定认为A优于C；或者是他认为A与B等优，B又与C等优，则A与C一定也等优。大家注意到，这跟数学上说两个数一定能进行比较，若非A>B，或B>A，就是A=B；而且这种大小关系可以传递，即若A>B（或A＝B），且B>C（或B＝C），必有A>C（或A＝C）的情况在逻辑上是相通的。在这两个公理的基础上就推出“偏好序列命题”，即“偏好定律”，说的是消费者能前后一致地按照偏好的顺序排列所有商品组合，这一序列用数学来表达就是“偏好函数”。

在以上的公理及定律之上，我们再加上一个“多比少好”的限定，即人对同一种商品的偏好是越多越好。这不是一个公理，因为有些东西是人不喜欢的，例如成本、垃圾等，这类东西人是希望它们越少越好。书上64页把“越多越好”的东西称为good（物品），把“越少越好”的东西称为bad（恶品）。但是，我们只需要做物品的分析，不需要做恶品的分析。因为一切的恶品，只要对它作适当的重新定义，就能转化为物品。例如“垃圾”这恶品，把它重新定义为“清理垃圾”就能转化为物品。“成本”就改成“减少成本”。这样，对物品的分析就能类推到对恶品的分析之上，不需要另外考虑针对恶品的特别分析。

这样，64页的图就把前述的内容以几何的形式表达出来。横轴和纵轴分别表示两种物品（即人认为是越多越好的东西）X和Y的数量，直角坐标系里的每一个点反映的是这两种物品的不同数量的组合。如A点的横轴坐标反映的是这个商品组合中X商品的数量，纵轴坐标反映的是Y商品的数量。根据上述的公理、定律及物品的定义，我们可以判断这图中的四个点A、B、C、D中，A点是最优的——因为它所反映的X和Y商品的数量都是最多的——，D是最差的，而B和C位于中间。这就是人对这四个商品组合进行了符合偏好序列命题所规定的偏好排列。但问题来了：B和C这两点，哪个比较好呢？它们之间怎么排列？B的Y商品数量比C多，在这方面比C好；但B的X商品数量比C少，在这方面又不如C了。显然，光是有前面的公理、定律及物品的定义，这理论的约束力还不够强，不足以对人的行为——他面临B和C时会选择哪一个商品组合，或者说他会怎么排列这两个商品组合——作出确定无疑的推断。

经济学家对这问题的解答是创造出“等优曲线”这分析工具，所以接下来我们就要学习等优曲线是怎么推导出来的。

先要学一个叫“效用”（utility）的概念。效用是什么？这个概念对于初学入门的人来说很难理解，但其实有一个很简单的方式去理解。那就是大家在中学的时候都在政治课里学过马克思的经济学。（顺便补充一句：马克思的经济学在习惯上称为“政治经济学”，其实那就是经济学，是古典经济学时期的称谓。因为Economics这个单词在亚当·斯密开创经济学这门学科之前就已经存在，其含义是“家庭理财”。古典经济学家为了让普通人能明白他们研究的不是家庭理财，而是国家理财——早期的古典经济学家确实认为他们研究经济学的目的是为了帮助国家理财，亚当·斯密的《国富论》顾名思义就是要探究国家财富或国民财富的性质与成因——，于是在Economics之前加上political（政治的）的限定词，于是古典经济学时期的人们习惯于把经济学称为“政治经济学”。到了新古典经济学时期，即使普通人也绝不会把Economics误会成“家庭理财”，于是马歇尔写他的《经济学原理》时索性把political这限定词给取消了，轻装上阵，直截了当就叫做Economics。到了现在，“经济学帝国主义”大行其道，“入侵”到政治学的研究领域，于是以经济学理论为工具来研究政治学问题的交叉学科又被冠以“政治经济学”之名。大家要了解经济学发展的历史，辨析清楚马克思时代的“政治经济学”与现在的“政治经济学”的含义是非常不同的。）

马克思的经济学里有一个叫“使用价值”（use value）的概念，这概念实际上并不是马克思发明的，而是亚当·斯密发明的，普遍地为古典经济学家所使用。这“使用价值”的概念只要作些修改，就完全等同书上所说的“效用”的概念。实际上，“效用”的概念最早是由英国哲学家边沁所发明的，他以其主张的“功利主义”——其实就是“效用主义”，这只是同一个词在哲学与经济学中翻译成中文的习惯译法不同而已——的哲学思想而得享大名。这概念被发起边际革命的经济学家引进经济学之后，就一举取代了亚当·斯密的“使用价值”的概念。然而，经过一番波折之后，经济学家已经完全改变了“效用”这概念最初在边沁那里的含义，与“功利主义”所主张的人的一切行为的目的是追求快乐、逃避痛苦已经毫无关系，而变成用来量度人对物品的偏好程度的工具。再追问下去：人为什么要偏好某个物品？当然是因为这物品能满足他的某种需要，于是……那无非就是说这物品对人有“使用价值”嘛！

但是，亚当·斯密（及马克思）所主张的“使用价值”的概念与现代经济学所主张的“效用”概念有一个重大区别，那就是前者是客观的，后者是主观的。在亚当·斯密（及马克思）看来，同一个物品对不同人而言，是有同样的使用价值的；但在现代经济学家看来，同一个物品对不同人而言，是可以有非常不同的效用的。所以，大家可以用你们在中学的时候已经学过的“使用价值”的概念直接套进这“效用”来理解，但必须作一个修改，那就是使用价值是主观的，不是客观的！

但是大家要注意，说使用价值是主观的，不等于说它是不真实的。举例来说，我手上拿着的这支水，对我来说使用价值很高，对你们来说使用价值却比较低，为什么？因为你们是听课的，不用说话；我是讲课的，要不停地说话。如果没有这支水，我的喉咙会很难受，你们却无所谓！所以这支水的使用价值会因人而异，但你不能说这支水的使用价值是虚无缥缈之物，毫无道理可言。另外，物品的使用价值还会因时因地而异。大家想象一下，如果你现在身处沙漠之中，身上没有带水，并且你估计再走上十天十夜也不会找到水源。这时有人拿着这么一支水出现在你面前，你愿意花多少钱去把它买下来？答案是：你会愿意把你身上所有的钱都拿出来交换！为什么？因为这支水的使用价值在这种情况下对你来说是非常非常的高，高得等同于你生命的价值！

说到这里，我还要补充一句，马克思（实际上是亚当·斯密为首的古典经济学家）还有一个叫“交换价值”的概念，并把它与价格区别开来。这种区别是毫无意义的。交换价值就是价格，它与使用价值是有关系的，但当然不是马克思的经济学主张的那种关系。价格（交换价值）与效用（使用价值）的关系我以后讲授到有关理论的时候再说，现在先按下不表。

（按：熟悉张五常教授的《经济解释》的朋友会注意到，我这里把使用价值的概念作了修正之后等同于效用的概念，与张五常教授所主张的以修正了的使用价值的概念取代效用的概念的做法不尽相同——其实我认为逻辑上是一样的，只是我考虑到效用这概念已经在经济学里根深蒂固，于是不说使用价值的概念取代它、而是等同于它，这跟我对“均衡”概念的处理也跟张五常教授不尽相同是类似的原因——，但我曾经当面问过张五常教授，他的使用价值的概念与效用的概念到底有何不同。他的回答是，效用是意图，不是事实；但使用价值是事实。我再追问使用价值怎么会是事实，他却没有再回答下去。我独自思考，想来想去都不觉得经张五常修正过的使用价值的概念，与效用的概念有何不同。你可以说效用是意图之物，但通过与金钱物品（在市场上可成交、因此可用货币来标示价格的物品）交换，这意图是可以用事实——与金钱物品交换的价格——反映出来的。你可以说使用价值是事实，但既然它是主观的，是因人、因时、因地而异的，如果不在具体的局限条件——那人、时、地的局限——下通过与金钱物品交换，也一样无法表达出来。而且，仔细地考察张五常教授用到这“使用价值”的概念，只有在分析消费者盈余的时候，其余时候都不会去用这个概念，跟一般的经济学家动不动就把效用概念乱用一通、因此作出的往往都是套套逻辑的解释相比，显得极其的小心谨慎。而分析消费者盈余时的使用价值或效用，原则上是可以通过拍卖的方式把它显示出来的，绝非无法观察的东西。所以，我不得不猜想，张五常教授认为使用价值的概念是事实，其实不是因为它与效用的概念有本质上的区别，而是如果只把它限于分析消费者盈余，以拍卖的方式就足以确保这个概念不会流于无法观察的意图之物。既然如此，面对效用这个概念在经济学里已经广为人知的局限，我的主张是保留它，但严格地将它限制在只用来分析消费者盈余。而对于中国学生来说，面对他们在中学时代已经学过马克思的使用价值概念的局限，却反而不如让他们直接以使用价值的概念——当然是要加以修正——来理解效用的概念。）

最初，经济学家认为效用是基数，但后来他们发现效用只能是序数。所谓基数就是1、2、3……，是可以进行加减乘除的四则运算的——如长度是基数，因此我们可以计算3米的绳子比1米的绳子长2米，并且这两条绳子连起来总共长4米。而所谓序数就是第1、第2、第3……，只能排序，不能进行加减乘除的四则运算——你说第1加第2是多少？不可能是第3吧？我们也无法比较不同序数之间的距离有多大。例如香港小姐选举，决出了冠军、亚军、季军这前三甲，我们可以肯定的只是理论上冠军应该长得比亚军漂亮，亚军又长得比季军漂亮，但冠军比亚军漂亮的程度，跟亚军比季军漂亮的程度相比，是更大还是更小还是一样？不知道！注意：由于序数只能排序不能运算，因此人们习惯于用基数来替代序数。比如说这香港小姐的选举，评委分别给各选手打分，那分数是基数，不但可以排序，还可以比较差距的大小。如冠军是获得90分，亚军获得85分，季军获得70分，这分数显示冠军与亚军之间的差距，比亚军与季军之间的差距要小。但这分数只是为了方便把选手在不同比赛环节中的表现加总起来得到一个最终结果再进行排序，实际上并不真的能反映冠亚季军之间的差距。当一个东西是序数，而人们为了方便运算、于是拿基数来替代它时，一定要非常小心，不能把基数运算中包含着的、序数所不具备的性质也错误地收纳进来。——事实上，效用理论之所以是充满了陷阱，除了前面已经提到过的效用是意图、不能直接用来解释事实、否则会陷于套套逻辑的错误之中的问题之外，也因为经济学家要用数学来表达效用时，很容易就会一下子忘记了效用是序数而非基数的本质，用了基数才能进行的四则运算去分析问题，于是中间的数学推导再正确无误也没用，因为从一开始这些分析就是建立在基数效用的错误基础之上而进行的。

效用是序数而非基数，那是因为效用（或使用价值）是主观的，无法进行人际比较。中国有一句古话叫“拔一毛以利天下而不为”，本来是形容极端的自私。但从经济学的角度来看，这一毛对要拔的那个人来说，他认为其使用价值就是很高很高，只要他不愿意跟天下人的利益（使用价值）交换，你不能强迫他，不能以天下人对这一毛的使用价值加总起来大于这一个人的使用价值而要求他非拔不可。这样，拔掉一毛的所谓“社会总效用”（以天下人对那一毛的使用价值加总起来减去那一个人的使用价值），在没有交换的情况下是无法计算出来的。我们能看到的只是，那一个人站在自己的立场上，把他保留这一毛（一个选择）的使用价值排列在为天下人拔掉这一毛（另一个选择）的使用价值之上。站在其他人或整个社会的角度，对此可能有不同看法，但这都没意义，因为效用或使用价值就是主观的！

有了这个效用（使用价值）的概念之后，我们再回头去看刚才那个对不同商品组合进行排列的问题。翻到书上71页，图3-7左图的直角坐标中的每一个点都是一个与众不同的商品组合，人可以对这些点（商品组合）给他带来的效用（使用价值）进行排序。根据前面的比较公理，人会觉得有些商品组合是等优的，把这些等优的商品组合的点（如A、B、C、D）连起来，就能画出一条曲线，这条曲线称为“等优曲线”（indifferent curve，很多中文教材将之直译成“无差异曲线”，但这“无差异”指的是效用无差异，并不是商品组合无差异，容易引起误会，因此意译为“等优曲线”是更准确的翻译）。

等优曲线的特征有四：第一，它的斜率为负，即向右下方倾斜。大家翻回到64页的图3-1，刚才我们已经分析过这图上的四个点，知道A点一定优于D点，因此把A、D两点连接起来的向左上方倾斜的线不可能是一条等优曲线。事实上，大家想象一下，如果X、Y商品都是越多越好的物品，增加其中一种商品的数量而还要保持效用不变，当然就要减少另一种商品的数量才行，所以效用一样的商品组合的点，肯定是沿着这两种商品一增一减的方向移动才有可能构成一条等优曲线出来。既然一种商品增，另一种商品减，则这条曲线的斜率当然是负的。

第二，两条等优曲线永不相交。这个用数学上的反证法就能证明。大家看书上71页的图3-6。先假设有两条相交的等优曲线U1与U2，它们交于A点。由于A点与S点同在U1的等优曲线上，即A点与S点等优；又由于A点与T点同在U2的等优曲线上，即A点与T点等优。根据前述的传递性公理，必有S点与T点等优，则这两个点应该位于同一条等优曲线上，但事实是它们是位于两条不同的等优曲线上，这说明前提错误，两条等优曲线是不可能相交的。

第三，直角坐标系上每个点都有等优曲线通过（这称为“等优曲线的完备性”）。这其实等价于前述的比较公理，由此可推出平面上实际上密密麻麻地分布着无数条等优曲线，并不是书上70页画的那样只有几条——这是因为如果把所有等优曲线都画出来，整个平面就会是一片漆黑——，或者可以这么说，每两条等优曲线之间总可以再画出一条等优曲线来，这跟两个实数之间总可以再找到一个实数是类似的逻辑。同一条等优曲线上的点的效用（使用价值）是一样的，但不同等优曲线上的点的效用（使用价值）当然是不一样的。那怎么比较大小呢？结论是：越远离原点的等优曲线被称为位置越高的等优曲线，所代表的效用水平（使用价值）就越高。这结论的证明如下：再看回书上的64页的图，假设B、C两点是位于同一条等优曲线上的，显然可以再通过A点画一条等优曲线，位置比B、C所在的那条更远离原点；也可以通过D点画一条等优曲线，位置比B、C所在的那条更靠近原点。前面我们已经分析过，A点优于B、C两点，所以A点所在的那条较远离原点的等优曲线所代表的效用水平（使用价值）较高；而B、C两点都优于D点，所以D点所在的那条较靠近原点的等优曲线所代表的效用水平（使用价值）较低。

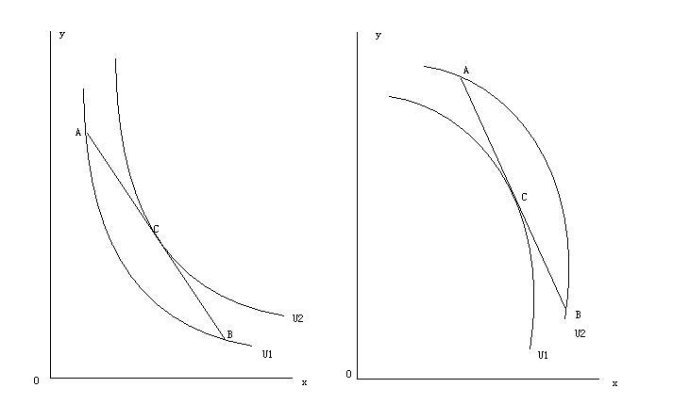
第四，等优曲线凸向原点。等优曲线是向右下方倾斜的曲线，但71页的图3-7的左图与右图都是向右下方倾斜，可是形状并不一样，左图是凸向原点，右图是凹向原点。左图含义着人喜欢“消费多样性”，而右图则含义着人喜欢“消费单一性”。大家我在黑板上画的图，左图里有一条U1的等优曲线，上面有A、B两点，把这两点以直线连起来，取中间的C点，过这C点可以作另一条U2的等优曲线，而U2所代表的效用水平（使用价值）是高于U1的，也就是C点的效用高于A、B点。显然，C点的商品组合中两种物品的数量都比A、B点的商品组合要均衡。这连接A、B点的直线后面我们就会知道，是两种物品的（相对）价格线（预算线），也就是在某一价格水平下，人会认为均衡地消费两种物品，比极端地消费其中一种物品（如A点是过多地消费Y商品，B点是过多地消费X商品）更为优胜。反之，右图里也有一条U1的等优曲线，上面也有A、B两点，把这两点以直线连起来，取中间的C点，过这C点也可以作另一条U2的等优曲线，但这时U2所代表的效用水平（使用价值）是低于U1的，也就是C点的效用低于A、B点。这说明在某一价格水平下，人会认为极端在消费其中一种物品，比均衡地消费两种物品更为优胜。显然，现实里的人的行为支持的是左图那种凸向原点的等优曲线。

以上就是等优曲线的四大特征。前面我们在第八讲的时候已经学习过互补品和替代品，它们的等优曲线在书上93页有画出来。完全替代品的等优曲线是直线，完全互补品的等优曲线是直角，这世上绝大部分的商品是位于这两个极端之间，因此一般情况下的两种商品的等优曲线是凸向原点的曲线。有关的分析很简单，我不细讲了，大家课后自行阅读92～94页的内容。

以上大家学了一大堆东西，还只是消费者理论对人的意图（偏好）的假设。要更进一步地求出消费者的最优选择（或所谓的消费者均衡），还得加上局限条件。因为等优曲线只是告诉我们以下信息：有些点（商品组合）是等优的（它们在同一条等优曲线上），越远离原点的等优曲线代表的效用水平（使用价值）就越高。站在人是自私的角度来看，再无其它局限条件的约束的话，人会选择无穷无尽地远离原点的那条等优曲线上的无数个点（商品组合）来消费。显然，这样的回答毫无意义，无助于我们推断消费者的行为。

于是，接下来大家要再学一条叫“预算线”（budget line）的东西，就是用来反映消费者进行消费选择时所面临的局限条件。大家看书上的84页的图。那阴影三角形的斜边就是预算线，是根据预算约束方程（84页的方程4-1）画出来的直线。这预算约束方程或预算线的经济含义是：消费者进行消费选择时所面临的局限条件有两个：一个是收入，一个是价格（X商品与Y商品的相对价格）。试想一下，如果没有收入有限的约束，消费者想买什么就能买什么，那他是不需要选择的，在自私与物品是越多越好的条件下，所有商品他都会消费无穷之多。或者是虽然收入有限，但如果物品是不需要支付任何价格就能买到的，则收入有限也不成为约束，消费者同样是会消费无穷之多的商品。就是收入有限，购买商品又要支付价格，消费者才需要考虑以下问题：我怎么把我的有限收入分配在不同的商品上进行消费，才是最有利于我的呢？所谓“最有利”就是“最优”，根据上述的偏好定律，消费者的最优就是寻求效用最大化——当然是有收入与价格约束下的效用最大化。

我们先来看这消费者最优选择（或所谓的消费者均衡）的几何解。从84页上的图可见，将预算线与等优曲线画在同一个直角坐标系中，大家就会发现，等优曲线与预算线的位置关系有三种：相交（如U1）、相切（如U2）与相离（如U3）。显然，相离（U3）的等优曲线最远离原点，代表着最高的效用水平（使用价值），是最有利于消费者的。然而，这条等优曲线虽然很好，可惜消费者到达不了！因为这条等优曲线与预算线相离，其经济含义是：等优曲线上的每一点（商品组合），在现有的价格水平与这消费者的收入水平的局限条件之下，都是这消费者买不起的。我也想住豪华别墅，我也想天天山珍海味、鱼翅捞饭（粤语俗话，意为鱼翅拌饭），我还想坐着渡轮环游世界……这世上多的是我想做的事情（直角坐标系的平面上多的是代表着很高的效用水平的商品组合的点），可惜我办不到！另外两条等优曲线中，相交（U1）的那条从Q点到R点的那段弧都是这消费者买得起的商品组合，但这条等优曲线位置太低，也就是代表的效用水平太差（是三条等优曲线中最差的），这消费者可没兴趣选择它。剩下的是相切的那条等优曲线（U2），上面有没有点是这消费者买得起的呢？有，只有一点，就是那切点C*！有一点就够了，那一点就是消费者的最优选择，因为这是消费者在现有的局限条件（收入与价格）之下所能达到的位置最高的一条等优曲线上唯一一个他买得起的商品组合！

以上是几何解，接下来我们看相应的代数解。既然几何解是等优曲线与预算线的切点，那么换成代数方式来表达的话，那就是求这两条线的斜率相等。预算线是直线，其斜率就是把相应的预算约束方程调整为等号左边只有y，其余各项移到等号右边去，整理出来的x的系数就是这预算线的斜率，那就是Px/Py，即两种商品的相对价格。而等优曲线的斜率呢？微积分知识已经告诉我们，曲线的斜率就是导数dy/dx嘛！在经济学中，等优曲线的斜率dy/dx称为“消费的边际替代率”，其经济含义是指为了增加消费其中一种商品的一个单位，在保持效用水平（使用价值）不变的前提下需要减少消费另一种商品的数量，也就是以其中一种商品的消费去替代另一种商品的消费的边际量。于是，dy/dx=Px/Py就是消费者最优选择（或所谓的消费者均衡）的代数解。

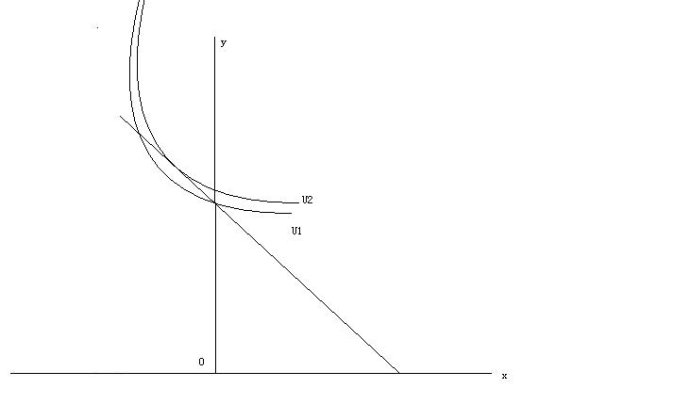
上述的几何解与代数解都是数学上所谓的“内角解”，但也会出现所谓“角点解”的情况。大家看黑板上的图。与预算线相切的等优曲线是U2，但切点位于负数域内，显然这在现实中不可能出现。于是消费者只好退而求其次地选择U1这条等优曲线，因为它是所有与预算线在正数域有交点的等优曲线中已经是最远离原点（也是最靠近U2）的了。U1与预算线的交点就是预算线与纵轴的交点，其经济含义是这个消费者所有的收入都花在Y商品上，X商品一点都不买（消费量为零）。现实中有大量的商品是我完全不购买的，例如豪华别墅、环球旅游等昂贵的商品，也有价格很便宜、但质量奇劣无比的商品，还有其它我认为对我完全没有使用价值的东西（如以马达加斯加语写的一本小说），它们都属于这种X商品。顺便说一句，有必要对X、Y商品作广泛的理解，如角点解时的X商品可理解为是所有你不购买的商品，而Y商品则可理解为X商品以外的其它所有你多多少少会买一些的商品。这样，这个看似十分远离现实的两商品模型就并不是那么不切实际了。

注意：上述的消费者最优选择的分析中隐含着一个局限条件，那就是这个模型所模拟的世界是没有借贷行为的。在现实生活中，人们不会把现在的所有收入就在现在全部花完——这通常不会是最优选择，而是会在现在消费与未来消费之间先做选择。这涉及到利息理论，也就是这教材的第十五章《时间经济学》才会讲授的内容，现在也是先按下不表。撇开在现在消费与未来消费之间进行选择的复杂性，现在的收入就得在现在全部花完，留到未来就全部腐烂、价值灭失（想象一下这收入是以新鲜蔬果来体现的），并且这个世界没有借贷——你也不能把现在的收入贷给别人用作现在的消费，换取未来他归还给你以满足你未来的消费；现在的消费也不能超过现在的收入，因为同样是由于没有借贷，你不能向别人借入他的现在收入以满足你超出现在收入水平的消费。

以上就是消费者理论的前半部分内容，后半部分是关于收入与价格这两个局限条件变化时消费者最优选择（或所谓的消费者均衡）的变化，并试图由此推导出需求曲线。后半部分的内容下一讲再介绍（并批判！），这里先要批判的是这一讲一开头时就已经指出的，很多经济学家所进行的效用分析，基本上都是套套逻辑，根本没有解释到任何现象！这里我就举这课本里的一个典型“反面教材”。大家翻到74～76页上的“应用：行善”，其分析可以说就是一个非常典型的、堕入了套套逻辑之中而不自知的效用分析。表面看起来，这分析很有道理，思维也显得极为聪明，但实际上只是用假设出来的所谓利己者的偏好或效用（以形状特别的等优曲线来反映）直接解释捐钱的行为，也就是说，这解释是假设出来的！所谓的人们愿意捐钱给比自己贫穷的人的行为，其实已经作为一种假设隐含在那等优曲线的形状之中（比利己者富有的人的收入是中性品，比利己者贫穷的人的收入是越多越好的物品），所以这实际上是直接使用假设（对等优曲线形状的假设，就是对利己者偏好于增加比自己贫穷的人的收入的假设）去解释人们愿意捐钱给比自己贫穷的人的行为。说白了，这等于是说：因为A是B，所以A是B！这不是套套逻辑，又是什么呢？然而，在漂亮的几何图形的包装之下，效用分析显得美仑美奂，再加上因为实际上是套套逻辑，所以结论一定是正确的，于是又显得似乎极是逻辑井然、推理严密。然而，若你有一双慧眼，能把这数学包装无情揭开，就会发现里面只是空空如也、实际上什么都没解释的壳子！

那么，怎么解释行善的现象才不是套套逻辑呢？其实我在第三讲里已经示范了如何以自私假设加上局限条件的变化来解释看起来并非源于自私的捐钱行为，大家可以回头细看那一段的解释，再跟课本上的这个以效用理论（等优曲线）的解释对比一下，好好地深入体会什么才是真正的解释，什么只是虚有其表的套套逻辑！

本讲课后作业：上一讲分析了房屋租赁市场上价格（房租）管制的后果，这一讲的作业就让大家分析一下房地产市场上数量管制（限购令）的后果。限购令实施以来，我们观察到的房地产价格的变动如下：先是几乎价格没有任何下跌，甚至一些市中心黄金地段的房价还小幅上升了；然后最近出现大幅下跌。解释这价格变动的现象，不准掺杂任何主观感情色彩的价值判断，否则一律删而不答！

上一讲作业的回答及评论选登：

（2）评论选登：

realme2011-12-12 17:54:44

再无情的市场也比再善良的国家好

lately_chou2011-12-12 17:55:45 

票价由市场决定会好过价格管制，不能接受高价格的人会有自己的安排，怎样安排都比排队好。

新浪网友2011-12-12 23:38:14 

在目前中国铁路的产权局限下，天下没有纯真的“公产”，天下无黄牛的“大治”违背了自私的假设！

如果将铁路资源彻底界定为私产（就象美国BURLINGTONG铁路公司那样），那么就可以借用麦克阿瑟的一句话，黄牛不死，they just fade away。

博主回复：2011-12-13 08:21:55

呵呵，最后一句很精彩。

发现各位读者现在的最后一句往往都有出彩的表现，我在考虑是否以后要加一个“最后一句精彩大奖”？

——本博客管理员

（说明：

1、这系列文章是本博客管理员（不是张五常教授！）根据给本科一年级的经济学专业学生讲授“微观经济学”、“宏观经济学”的授课内容而整理出来的讲义。使用的主干教材是张五常教授的老师赫舒拉发所编写的《价格理论及其应用》，并在授课过程中将张五常教授的旧版《经济解释》三卷本有机地结合进来，是本博客管理员在实际的经济学教学之中探索将张五常经济学透过主流教科书传授给经济学学生的成果。

2、本系列不定期更新，甚至可能写着写着会因兴趣缺缺而中止，本博客管理员对此不作任何担保！

3、如有愚蠢无知、明显缺乏科学逻辑的评论，一律不予回答，只作删除处理。另外，不看完这个系列最新更新之前的以往所有文章就急于提问，提问内容其实早在前面的文章中给出了回答的，也是一删了之！）